分子動力学法

　分子動力学法（Molecular dynamics method）とは， 系を構成する粒子（原子）の運動方程式を差分法により数値的に時間積分することで， 各粒子の位置と速度の時間変化を得る方法である． 各粒子にはポテンシャル関数Uによって記述される相互作用力が働く． 運動方程式はNewtonの運動方程式である．

(1)\[m \frac{d^2}{dt^2}\boldsymbol{r}_i = -\nabla _i U(\boldsymbol{r}_1,\boldsymbol{r}_2,....\boldsymbol{r}_n)\]

まずは二体ではじめよう．

Lennard-Jonesポテンシャル

アルゴン原子の衝突過程を計算してみよう． アルゴンの原子間には，van der Waals力が働く．van der Waals力はLennard-Jonesポテンシャルで記述できる．

原子　\(i\)　と原子　\(j\)　の間のLennard-Jonesポテンシャルは，

(2)\[U_{LJ}(r_{ij}) = 4 \epsilon \left[\left(\frac{\sigma}{r_{ij}}\right)^{12} - \left(\frac{\sigma}{r_{ij}}\right)^{6} \right]\]

ここで，\(r_{ij}=|\boldsymbol{r}_i-\boldsymbol{r}_j|\) で原子iとjの距離である．

原子1と2がある場合，1に働く力は，

\[\begin{split}-\nabla _1 U(\boldsymbol{r}_1,\boldsymbol{r}_2)&=-\frac{\partial}{\partial \boldsymbol{r}_1} U_{LJ}(\boldsymbol{r}_1,\boldsymbol{r}_2)=-\frac{\partial}{\partial \boldsymbol{r}_1} U_{LJ}(r_{12})\\ &= -\frac{\partial}{\partial r_{12}} \frac{\partial r_{12}}{\partial \boldsymbol{r}_1}U_{LJ}(r_{12})\\ &= -\frac{\partial}{\partial r_{12}} \left[-4 \epsilon \left[ \left(\frac{\sigma}{r_{12}}\right)^{12} - \left(\frac{\sigma}{r_{12}}\right)^{6} \right] \right]\frac{\partial r_{12}}{\partial \boldsymbol{r}_1}\\ &= 4 \epsilon \left[ -12\left(\frac{\sigma}{r_{12}}\right)^{12}\frac{1}{r_{12}} +6 \left(\frac{\sigma}{r_{12}}\right)^{6}\frac{1}{r_{12}} \right] \frac{\boldsymbol{r}_1 - \boldsymbol{r}_2}{r_{12}}\\ &= 24 \epsilon \left[ \left(\frac{\sigma}{r_{12}}\right)^{6}\frac{1}{r_{12}}-2\left(\frac{\sigma}{r_{12}}\right)^{12}\frac{1}{r_{12}} \right]\frac{\boldsymbol{r}_1 - \boldsymbol{r}_2}{r_{12}}\end{split}\]

---

ただし，

\[\begin{split}\frac{\partial r_{12}}{\partial \boldsymbol{r}_1} &= \left( \frac{\partial r_{12}}{\partial x_1},\frac{\partial r_{12}}{\partial y_1},\frac{\partial r_{12}}{\partial z_1} \right)\\ \frac{\partial r_{12}}{\partial x_1} &= \frac{\partial}{\partial x_1} \sqrt{(x_1-x_2)^2 + (y_1-y_2)^2 + (z_1-z_2)^2}\\ &= \frac{1}{2} \left[(x_1-x_2)^2 + (y_1-y_2)^2 + (z_1-z_2)^2 \right]^{-1/2} 2(x_1-x_2)\\ &= \frac{x_1-x_2}{r_{12}}\\ \frac{\partial r_{12}}{\partial \boldsymbol{r}_1} &= \frac{\boldsymbol{r}_1 - \boldsymbol{r}_2}{r_{12}}\end{split}\]

---

上式の大括弧内は　\(r_{12}=2^{1/6}\sigma\) の時にゼロになる．つまりこのとき1と2の間に力は働かない． またこの時，ポテンシャル \(U_{LJ}(2^{1/6}\sigma)=-\epsilon\) である． \(\epsilon\) はポテンシャルの最小値，谷底を表す．

\(r>2^{1/6}\sigma\) の範囲では6乗の項の効果が比較的強い． 力は正勾配で，二体間の距離が小さくなろうとするとき引力が働いて，さらに距離を小さくしようとする． \(r<2^{1/6}\sigma\) の範囲では12乗の項の効果が強くなる． 力は負勾配で，二体間の距離が小さくなろうとするとき斥力が働いて，反発しよう，距離を拡げようとする．

　\(R=2^{1/6}\sigma\) とすれば　(2) は，

\[U_{LJ}(r_{ij}) = \epsilon \left[\left(\frac{R}{r_{ij}}\right)^{12} - 2\left(\frac{R}{r_{ij}}\right)^{6} \right]\]

と，書ける．以下のコードはこちらの表記を元に作成した．

Note

Lennard-Jonesポテンシャルの6乗の項は引力項で，これがvan der Waals力に由来する．これに対して12乗の項は斥力項で，近づきすぎた原子を反発させる役割がある．この項の形は数値計算上の便利（6乗の2乗である）から決めらており物理的な由来はない（だったはず？）．

原子の衝突

まずは，以下は計算条件，初期条件の入力部と無次元化部分である． 惑星の世界とは反対に，原子の世界は非常に小さな値を扱うことになる． やはり無次元化をする．

program md
use globals
implicit none

call CPU_TIME(start_time)
!----- properties of atom
mass(1) = 6.63d-26
vdw_radii(1) = 2.0d0**(-1.0d0/6.0d0)*3.4d-10/2.0d0
vdw_welii(1) = 1.65d-21
mass(2) = mass(1)
vdw_radii(2) = vdw_radii(1)
vdw_welii(2) = vdw_welii(1)
rcut = 10.0d0*vdw_radii(1)

!----- initial conditions
coord(1,1) = -vdw_radii(1)*3.0d0
coord(2,1) = vdw_radii(1)*2.5d0
coord(3,1) = 0.0d0

coord(1,2) = vdw_radii(1)*3.0d0
coord(2,2) = 0.0d0
coord(3,2) = 0.0d0

veloc(1,1) = 0.5d2
veloc(2,1) = 0.0d0
veloc(3,1) = 0.0d0

veloc(1,2) = -0.5d2
veloc(2,2) = 0.0d0
veloc(3,2) = 0.0d0

!----- time
t = 0.0d0
tmax = 1.0d-11

!----- normalizse
cnor = vdw_radii(1)
mnor = mass(1)
enor = vdw_welii(1)
vnor = sqrt(enor/mnor)
tnor = cnor/vnor

coord = coord/cnor
veloc = veloc/vnor
mass = mass/mnor
t = t/tnor
tmax = tmax/tnor
vdw_radii = vdw_radii/cnor
vdw_welii = vdw_welii/enor
rcut = rcut/cnor

速度ベルレ法の部分に変更はない．van der Waals半径(R,vdw_radii)は，半分の値で入力している． 異種原子を扱う場合のパラメータをLorentz-Berthelot則にしたがって計算するためである． 二個のアルゴン原子を配置し，初期速度（50m/s）で互いに近づく．ただし高さ方向の初期位置に少々ずれがあるので，正面衝突ではない．

力とエネルギーの計算部分は以下のようにした．

!+++++++++++++++++++++++++++++++++++++++++++++++
module cal_ene

use globals
use param_particle
implicit none

contains
    subroutine cal_kin(v,e)
        double precision,intent(in)::     v(ndim,nbody)
        double precision,intent(out)::    e
        integer     i,j
        double precision    v2

        e = 0.0d0
        do i=1,nbody
            v2 = 0.0d0
            do j=1,ndim
                v2 = v2 + v(j,i)**2
            end do
            e = e + 0.5d0*mass(i)*v2
        end do
    end subroutine cal_kin
end module cal_ene
!+++++++++++++++++++++++++++++++++++++++++++++++
module cal_force

use globals
use param_particle
implicit none

contains
    subroutine force(c,a,e)
        double precision,intent(in)::       c(ndim,nbody)
        double precision,intent(out)::      a(ndim,nbody)
        double precision,intent(inout)::    e
        integer     i,j,k
        double precision    rij(ndim)
        double precision    rij_abs2,rij_abs,inv_rij_abs,inv_rij_abs2
        double precision    vdw_radij,vdw_welij
        double precision    rtmp2,rtmp6,rtmp12
        double precision    potij
        double precision    ftmp
        double precision    fij(ndim),f(ndim,nbody)

        f = 0.0d0
        e = 0.0d0
        do i = 1,nbody-1
            do j = i+1,nbody
                rij(:) = c(:,i)-c(:,j)
                rij_abs2 = 0.0d0
                do k=1,ndim
                    rij_abs2 = rij_abs2 + rij(k)**2
                end do
                rij_abs = sqrt(rij_abs2)
                inv_rij_abs = 1.0d0/rij_abs
                inv_rij_abs2 = 1.0d0/rij_abs2
                if(rij_abs .le. rcut) then
                    vdw_radij = vdw_radii(i) + vdw_radii(j)
                    vdw_welij = vdw_welii(i) * vdw_welii(j)
                    vdw_welij = sqrt(vdw_welij)
                    rtmp2 = inv_rij_abs2 * vdw_radij * vdw_radij
                    rtmp6 = rtmp2 * rtmp2 * rtmp2
                    rtmp12 = rtmp6 * rtmp6
                    potij = vdw_welij * (rtmp12 - 2.0d0 * rtmp6)
                    ftmp = 12.0d0 * vdw_welij * (rtmp12 - rtmp6) * inv_rij_abs2
                    fij(:) = ftmp*rij(:)
                    f(:,i) = f(:,i) + fij(:)
                    f(:,j) = f(:,j) - fij(:)
                    e = e + potij
                end if
            end do
        end do
        do i = 1,nbody
            a(:,i) = f(:,i) / mass(i)
        end do
    end subroutine force

end module cal_force

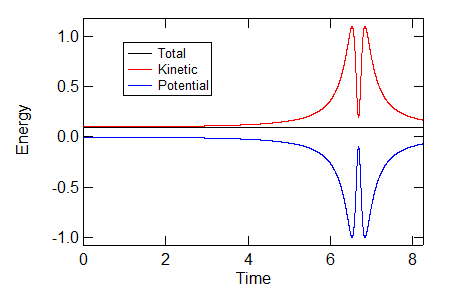
以下は，このエネルギーの変化である．

全エネルギー（運動エネルギー＋ポテンシャルエネルギー）は一定である．

原子が近づくにつれて，ポテンシャルエネルギーは谷に落ち込む．谷を越えてさらに近づくと斥力項の効果により上昇する．

斥力によりついには反発して，互いに遠ざかっていく．

運動エネルギーは，反対にポテンシャルエネルギーによる加速により増加し，反発による速度反転を経て逆向きに飛び去る．

動画をYoutubeに掲載した． >>Youtube3

エネルギーの初期値からの変動のステップ数依存は以下の通り．

衝突の前後で誤差が大きくなる．

1ステップを更新する毎のエネルギー変化の平均値を計算したところ，時間刻み10分の1で誤差は1000分の1になった（n=10⁷ 以外で）