周波数解析

　周期的な変動成分をもつ実験データから，その周期性に関する情報を取り出したい．ということがよくある． そのような場合，まずはフーリエ変換（Fourier transform）という技術がよく用いられる．pythonでやってみよう．

フーリエ変換

検索などをして調べてみると，scipyにfftpackいうモジュールが見つかる． 　>> SciPy fftpack

フーリエ変換の詳細はどこかで勉強するとして．．． 以下がサンプルコードである． 疑似的に三角関数の足し算で作られる周期的なデータ（f(x)）を用意し， このデータをフーリエ変換で周波数解析する．

Note

（参考文献） 科学計測のためのデータ処理入門 ，河田聡編著（CQ出版，2002）

Note

fftとはfast Fourier transformの頭文字である．和訳はそのまま「高速フーリエ変換」である．その名の通り，フーリエ変換を高速に(短時間に）行うアルゴリズムである．

import numpy as np
import matplotlib.pyplot as plt
from scipy import fftpack

def f(x):
    pi2 = 2.*np.pi
    return 1.0*np.sin(0.1*pi2*x) + 1.0*np.cos(1.*pi2*x)

#Periodic data with/without random noise
xdata = np.linspace(0, 100, num=1024)
np.random.seed(1234)
ydata = f(xdata) #+ 10.*np.random.randn(xdata.size)

time_step = xdata[1]-xdata[0]

#FFT
sample_freq = fftpack.fftfreq(ydata[:].size, d=time_step)
y_fft = fftpack.fft(ydata[:])
pidxs = np.where(sample_freq > 0)
freqs, power = sample_freq[pidxs], np.abs(y_fft)[pidxs]
freq = freqs[power.argmax()]

#PLot
plt.figure(figsize=(8,10))
plt.subplot(211)
plt.plot(xdata,ydata,'b-', linewidth=1)
plt.xlabel('Time')
plt.ylabel('Ydata')
plt.grid(True)

plt.subplot(212)
#plt.semilogx(freqs, power,'b.-',lw=1)
plt.loglog(freqs, power,'b.-',lw=1)
plt.xlabel('Frequency')
plt.ylabel('Power')
plt.grid(True)

plt.show()

５～７行目：周期的な関数． \(f(x)=1.0\sin(0.1*2\pi*x)+1.0\cos(1.0*2\pi*x)\) である．

１０～１２行目：f(x)を使って，データを作る．xは，0~100まで1024個のデータ．yは，xをf(x)に入れて計算．あるいはさらに雑音を加える．

１７～２１行目：fftの本体（特に１８行目）．

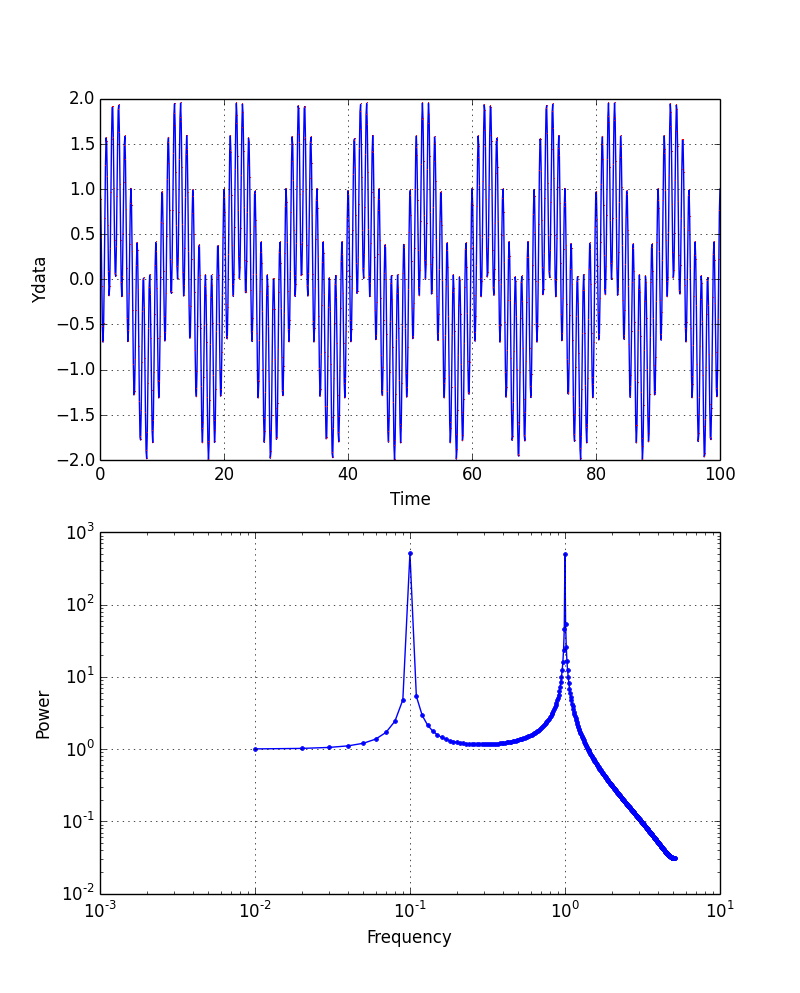
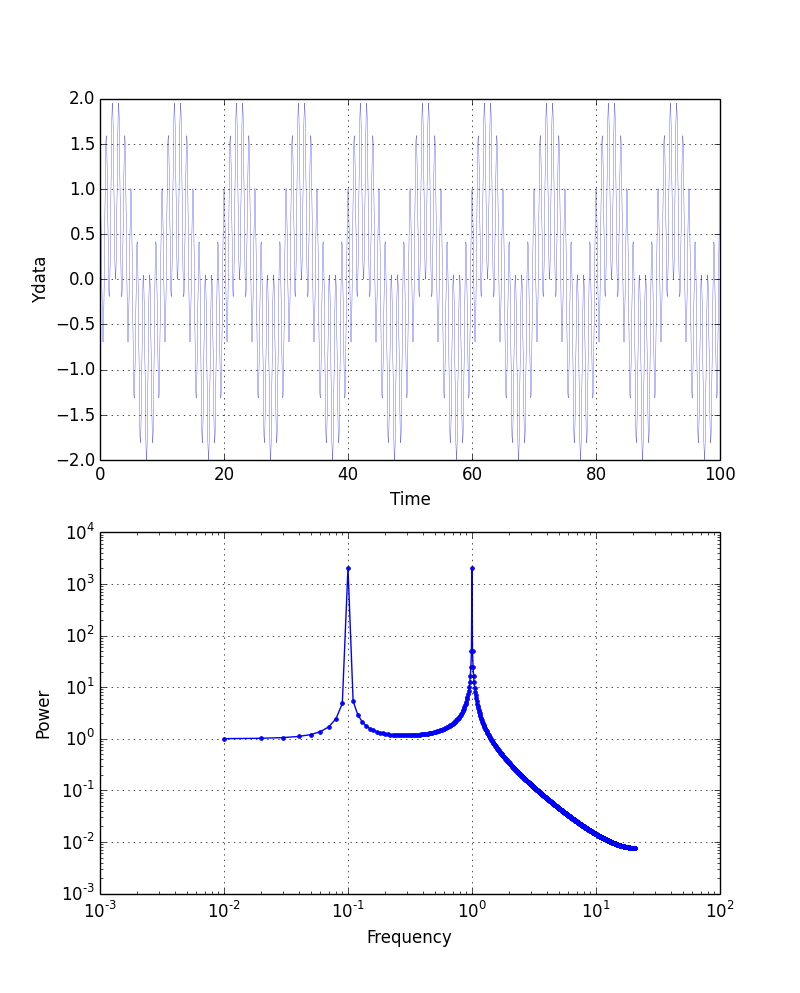
実行結果は以下の通り， 元のデータと，周波数解析結果の両対数表示を行う．

元の関数は，　\(0.1*2\pi*T = 2\pi\) と　，\(1.0*2\pi*T = 2\pi\) とで1周期の関数の足し算である． つまり二つの周期T =　10　と 1s（時間の単位が秒だったなら）をもつ．周波数（1/T）でいえば，0.1と1Hzである． 上の周波数解析結果をみると，ちょうど横軸が0.1と1Hzにするどいピークがあるのがわかる． 周波数解析を行うことで，元のデータが持っている周波数に関する情報が分かる．

解析の結果をきちんと解釈するためには， フーリエ変換の理論的な側面をしっかり勉強するのが一番だと思うが， ここでは，元のデータをいろいろいじって何が起きるかを見る．経験的に慣れよう．

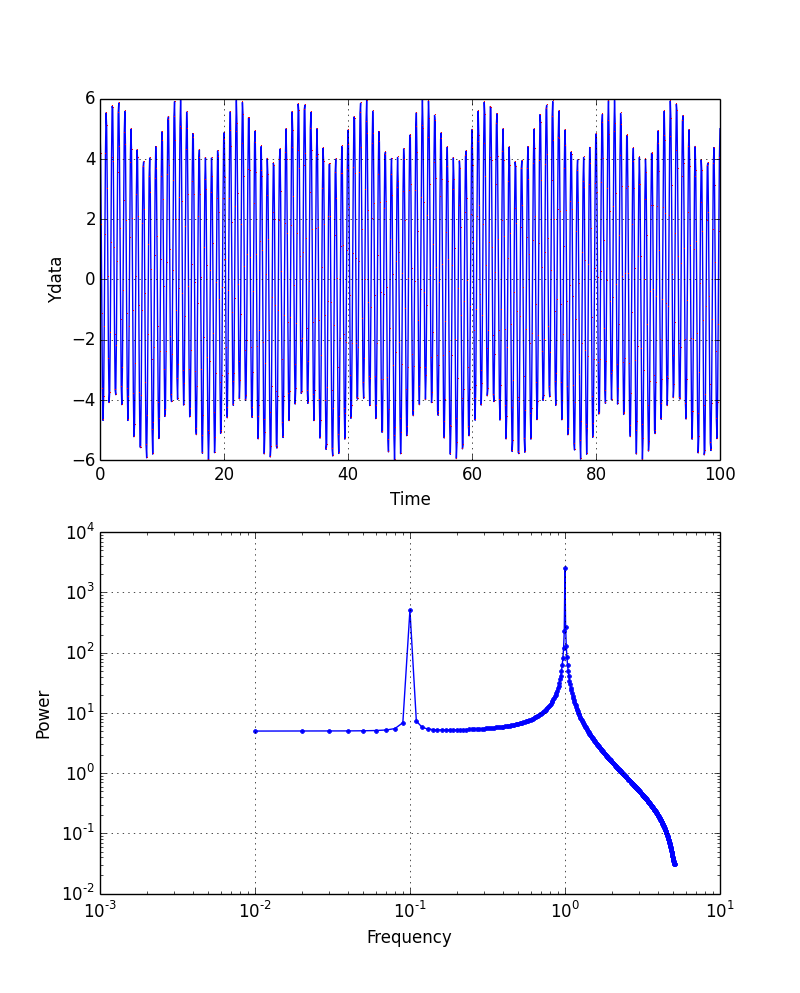
return 1.0*np.sin(0.1*pi2*x) + 5.0*np.cos(1.*pi2*x)

振幅を大きくすると

1[Hz]の成分の振幅を5倍に．

1[Hz]のピークが大きくなる．

return 1.0*np.sin(0.1*pi2*x) + 1.0*np.cos(10.*pi2*x)

振動数が変わると

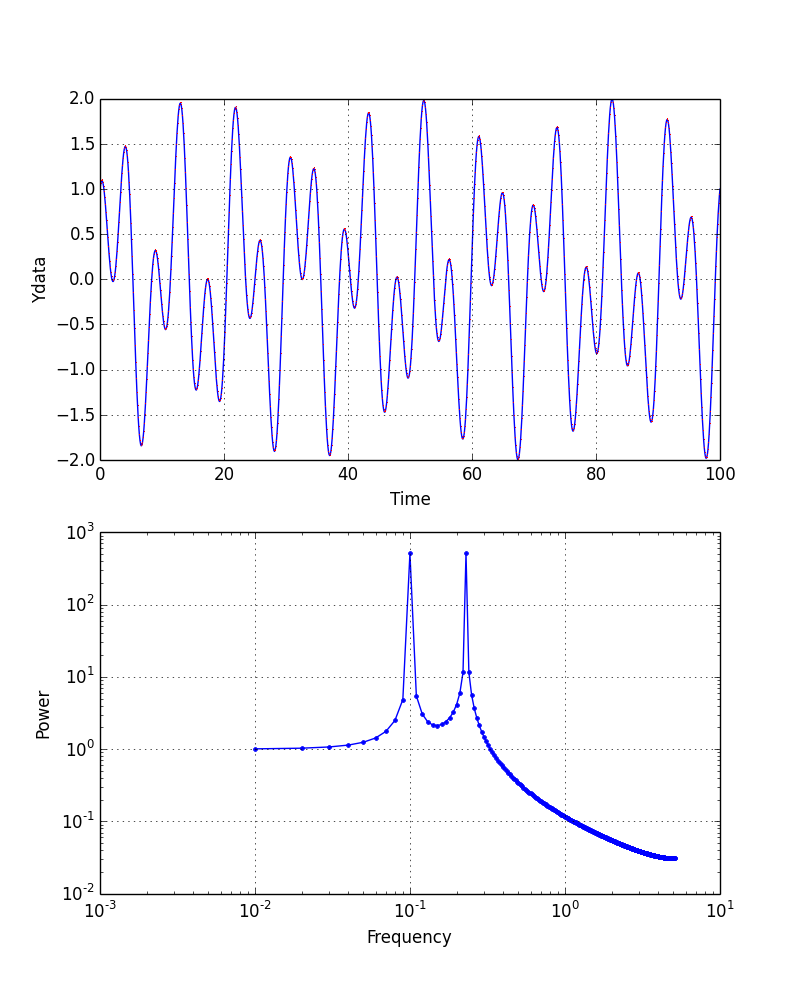
1[Hz]の成分を10[Hz]に

あれ？1Hzが消えて10Hzにピークが立つはずだが？0.2Hz付近にピークがある． おかしい？？ところで，これまでの図で横軸の最大値は5Hz前後である． そもそも10Hzまでプロットできていない． もともと100秒のデータを1024分割している．つまり，10.24Hzの周波数でデータを得ている． このあたりが原因か？

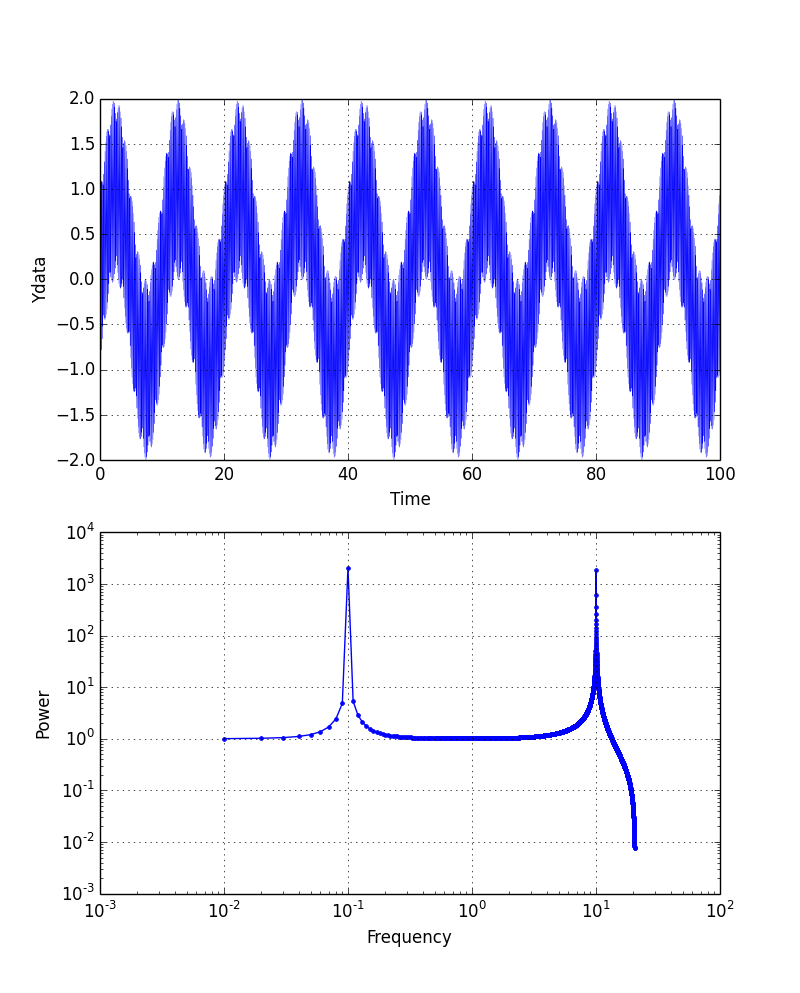
xdata = np.linspace(0, 100, num=4096)

そこで，横軸のデータ点数を増やしみよう．num=1024から4096（40.95Hz）に増やした． これは実際の実験ではサンプリング周波数（サンプリング速度）を上げたことに相当する．

横軸の最大値が20Hzまで広がり，無事10Hzにピークが現れる． ※線が太いとみずらいので，26行目は「plt.plot(xdata,ydata,’b-‘, linewidth=0.2)」に変更している．

そもそも二つ上のグラフは元データのグラフと形が違う．サンプリング周波数が十分ではなかった． 一般にサンプリング周波数は元となる信号の周波数の2倍以上ではないといけないとが知られている（サンプリング定理）． 2倍以上ではない時は元の信号の周波数（10Hz）とサンプリング周波数（10.24Hz）の差（0.24Hz）が現れる．これをエイリアス（折り返しひずみ）現象という．

Note

普通は元となる信号の周波数成分を知らないから周波数解析をするのである．上記のようなエイリアス現象による偽のピーク（0.2Hz）が得られたとき，何をもって偽と判断すればよいか？一つの方法は，なんだか原因が分からないピークが気になったらサンプリング周波数を変更してみることである．エイリアスが原因であればサンプリング周波数によってピークの場所が変わるはずである．．

念のため初めの係数で，num=4096の結果も示そう．

最初の図と比べると，0.1と1Hzにピークが現れることは変わらいが，ピークがより大きく（するどく）なっている．

元データの長さ

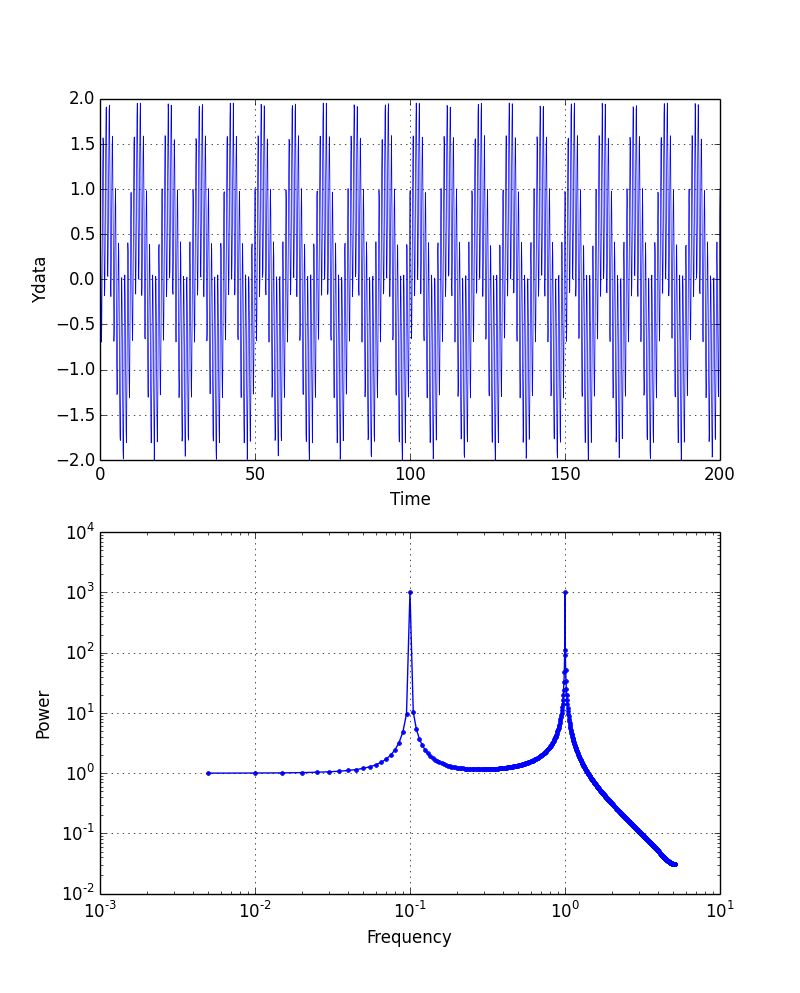
次に，サンプリング速度は同じままデータ収録時間を長くしてみよう．xdataの上限を200にし，データ数も2倍にする．

xdata = np.linspace(0, 200, num=2048)

横軸の最小値が0.001Hzから0.0005Hzに変わった．

データに雑音（不規則な信号）が加わるとどうなるか？

xdata = np.linspace(0, 100, num=1024)
np.random.seed(1234)
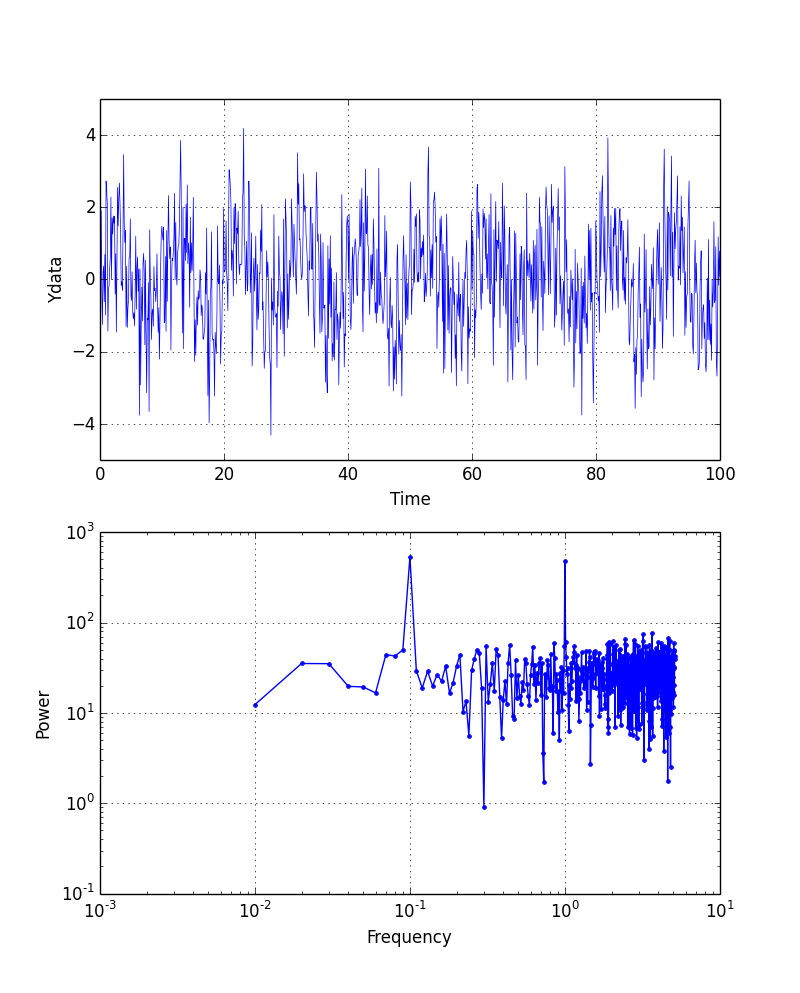
ydata = f(xdata) + 1.0*np.random.randn(xdata.size)

なんとか二つのピークは見いだせる．

しかし雑音が大きくなると，

xdata = np.linspace(0, 100, num=1024)
np.random.seed(1234)
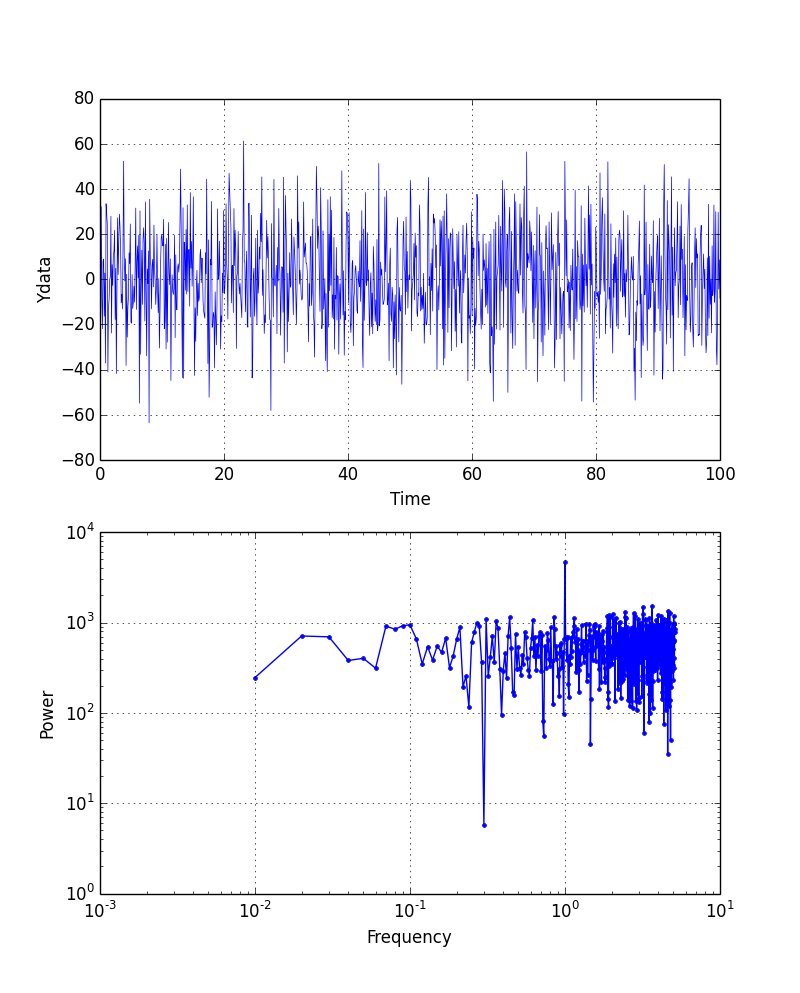
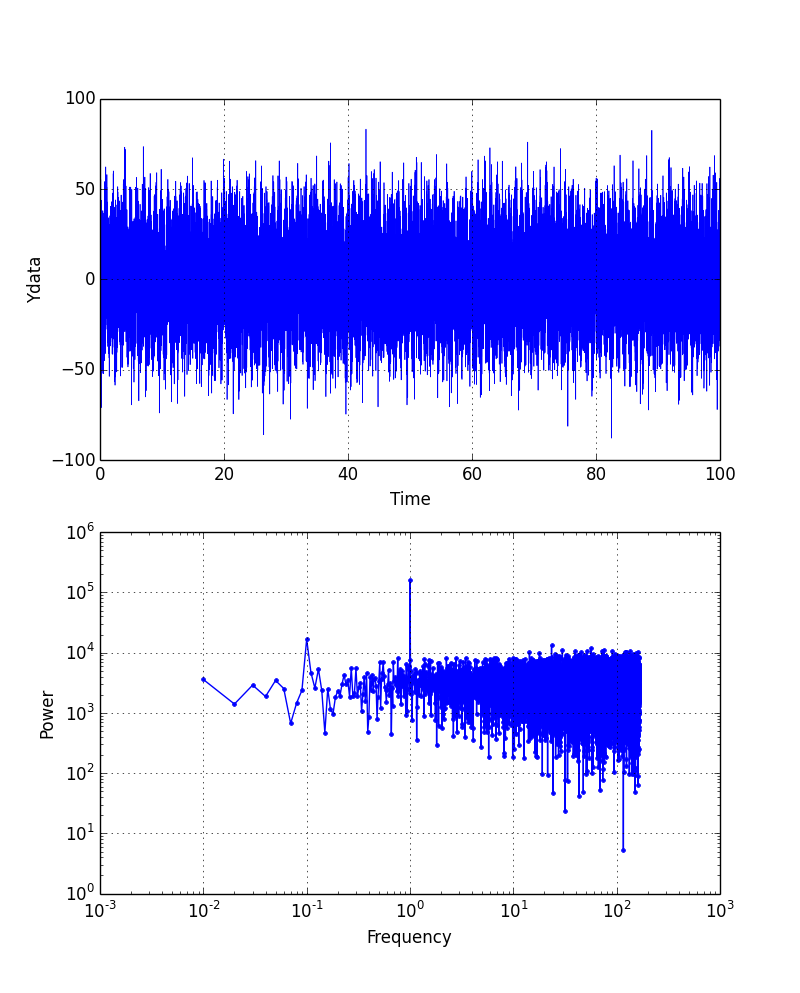
ydata = f(xdata) + 20.0*np.random.randn(xdata.size)

低い方の周波数が雑音に埋もれてしまった．

サンプリング周波数を（かなり）上げると，

xdata = np.linspace(0, 100, num=32768)
np.random.seed(1234)
ydata = f(xdata) + 20.0*np.random.randn(xdata.size)

再びピークが現れる．

Warning

フーリエ変換が有効なのは周期性のある情報に対してのみである．繰り返さない信号をフーリエ変換してもしょうがない．