例題：ファン・デル・ポール振動子¶

　ルンゲ－クッタ法では，エネルギーは保存しないが，非常に長時間にわたって計算が行えることが分かった．これを使って，ファン・デル・ポール（van del Pol）方程式の計算を行ってみよう．

ファン・デル・ポール方程式は，非線形力学の分野で有名な方程式である．

\[\ddot x + \mu\left(x^2-1\right)\dot x+ x = 0\]

ほとんど，バネ・マス・ダンパ系の方程式であるが，ダンパの部分（減衰項）が非線形になっている． \(|x|>1\) では減衰項が抵抗として働く（振動を小さくしようとする）が， \(|x|<1\) では，負の抵抗として働く．振動を大きくしようとする．

プログラムをほんの少々変更すれば計算できる．

以下の図は，　\(\mu=1.5\) , \(x(0)=0.5，v(0)=0.0\) の初期条件で計算を行った結果である． [tmax = 30.0d0，n=3000（時間刻みは0.01）]

位置の時間変化．振動がひしゃげている．

速度の時間変化．

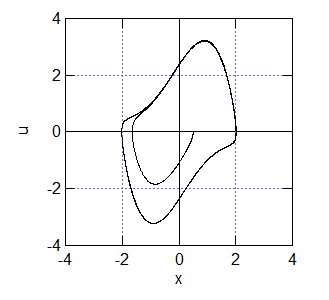
縦軸速度，横軸位置の相平面．

次は，　\(\mu=0.1\) , \(x(0)=0.1，v(0)=0.0\) の初期条件で計算を行った結果である． [tmax = 3000.0d0，n=300000（時間刻みは0.01）]

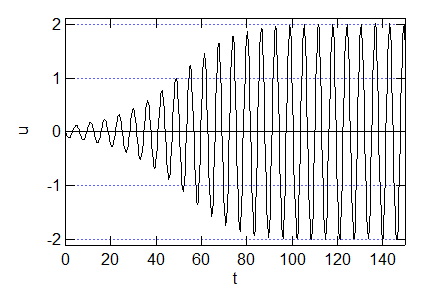
位置の時間変化．

速度の時間変化．位置，速度ともに徐々に振動が大きくなり，その後周期的な振動を維持する．

縦軸速度，横軸位置の相平面．原点近くからスタートして，徐々にほぼ円形の軌道に漸近していく．この軌道をリミットサイクルという． \(\mu\) が小さいときは単純な調和振動子に近い振舞いをする．調和振動であれば相平面は円である．

Note

〔ストロガッツ　非線形ダイナミクスとカオス　，Steven H. Strogatz,田中久陽ら訳（丸善出版，2015）〕