~おまけ~
「ぬるい.簡単すぎる」という学生さんへ
内容が「ぬるい」と感じた方は,次のプログラムにトライしてみてはいかがでしょうか?
-プログラム①-
関数f(x)=exsin5x のグラフを書くプログラムを作る.
xが-1から1まで,16ステップで変化するとして,関数f(x)を計算し,端末上にグラフとして示す.
普通に計算すると以下のように関数f(x)は,だいたい-3~2の間の数字を取る.
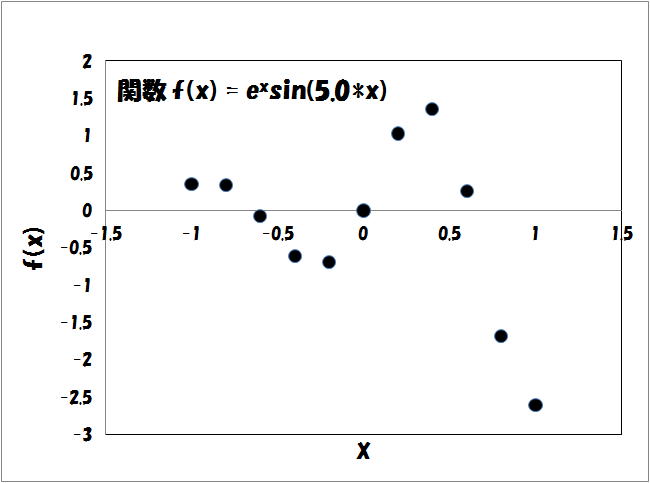
図1:関数f(x)のグラフ
さて,端末上でこのグラフを書いてみたい(普通はそんなことしませんが)というとき,どうすればよいか?
グラフは回転してしまうが,write文を使って以下のようなイメージでプロットできればOK.
図2:フォートランでグラフを書くときのイメージ.
白い部分は空白を書いて,赤いところに例えば”*”を書けば,グラフになる.
つまり上図の場合,1行目で7個の空白,その直後に*を表示させていることになる.
ここから少し具体的なプログラミングを考える.
(宣言文)
parameter(n=16)
real c,dx,x,y,xmin,xmax,ymin,ymax
real,dimension(0:n) :: yy,yy2
※dxは1ステップの間隔,xmin/xmaxはxの最小値,最大値でここでは-1と1である.
yyは関数f(x)の値が入る変数とする.
yyは実数形式で,ディメンジョン(領域)を0~nまでにしている.
変数yy2も変数yyと同じ.これを宣言する理由は後で明らかになる.
(メイン1)
”*”を表示させる場所は,関数f(x)に依存する.
しかし図1でわかるようにf(x)は-2~3の間で変化し,その値は当然実数.
一方,フォートランというよりあらゆるプログラミング言語では,
「変数内の1個目,2個目に数字を代入する」ことはできても,
「1.5列目に数字を代入する」なんて概念はない.
※real data(10,10) と変数を宣言しても,変数内の番地は必ず整数でしか表せない.
従って関数f(x)の値そのものを使うことはできなくはないが,
できたとしても非常に粗く,しかも歪曲されたグラフになる.
なぜなら関数f(x)の値はせっかく実数形式で計算しているのにも関わらず,
整数では-3,-2,-1,0,1,2でしか表せないからである.
しかも変数内の番地に,負の値は存在しない.かならず1もしくは0以上である.
そこでグラフを書く場合は,グラフの形さえ維持されていればいいのだから,
関数f(x)の値を無理矢理0以上の値,かつ
ある程度グラフの形を分解できる範囲にしてやる.
例えば,関数f(x)の値を,0~60の値に正規化する.
順番としては,
0) 関数f(x)の計算をする.
yy(i)=exp(i)*sin(5.0*i)
上式をDOループで制御すればよい.これでyyに関数f(x)の値が代入される.
1) 関数f(x)の最小値・最大値を検索する.
検索して,yminに最小値を,ymaxに最大値を代入しておく.
2) 「関数f(x)の値全て」に「最小値の絶対値」を足す.これで最小値は「0」になる.
最小値の絶対値は,abs関数を使う.(ex) abs(ymin)
3) さらに「関数f(x)の値全て」に適当な係数を掛ける.たとえば係数c=50/(最大値-最小値)を掛ける.
yy2(i)=yy(i)*c
これもDOループで制御する.
(メイン2)
最後に端末に書き込む.
変数yy2は実数形式なので,わざと整数型に変形する.
iy=int(yy2(i))
write(*,'(1x,63a1)') (' ',j=0,iy),'*'
これもDOループで制御する.このWrite文は「一文字の空白 + iy個の空白 + ”*”」を書き込む,という意味になる.
実行すると,
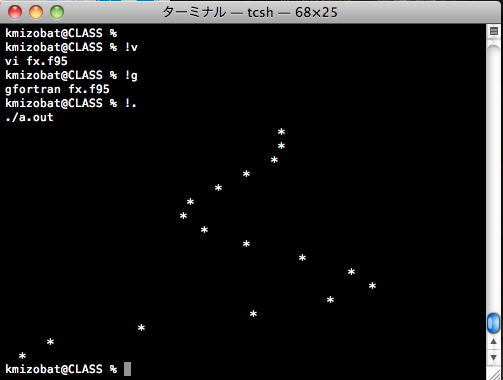
このようになる.
-プログラム②-
後半最後で行う地衡流計算は,海面高度勾配だけではできない.
必要なのはコリオリパラメータ,海面高度,そして距離である.
地球上での距離の計算方法は以下の通り.
(http://www.cs.nyu.edu/visual/home/proj/tiger/gisfaq.html より.)
Haversine Formula (from R.W. Sinnott, "Virtues of the Haversine",
Sky and Telescope, vol. 68, no. 2, 1984, p. 159):
ある地点A(Lat1(緯度)),Lon1(経度))からある地点B(Lat2,Lon2)までの距離は次のように求められる.
dlon = lon2 - lon1
dlat = lat2 - lat1
a = (sin(dlat/2))2 + cos(lat1) * cos(lat2) * (sin(dlon/2))2
c = 2 * arcsin(min(1,sqrt(a)))
d = R * c
※Rは地球の半径 6378.137 km

