2.相関係数とは
2つのデータセットが与えられた時、散布図を書くとなんとなく右肩上がりや左肩上がりの分布が見える時がある。
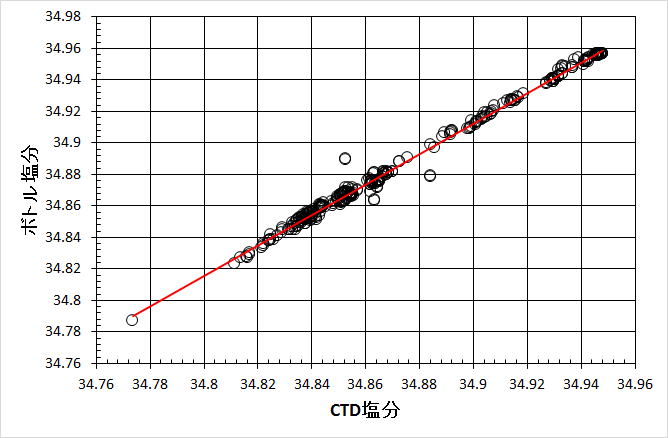
たとえばいま使っているデータでは、CTDの塩分(3列目)とボトル塩分(4列目)を用いて散布図を書くと、
明らかに右肩上がりの分布図が見られる(図1)。
これは2つの変量の間に「正の相関」があることを示している。
※ただしこれだけではセンサーの精度がよいということにはならない。
①平均値を求める
goukei=0
do k=1,345
goukei =goukei+csal(k)
enddo
heikin=goukei/345
②残差平方和を求める→「各データの平均値からのズレ」の二乗の総和
bunsan=0
do k=1,345
bunsan=bunsan+(csal(k)-heikin)**2
enddo
③分散を求める→残差平方和をサンプル数で除算
bunsan=bunsan/345
基本的に上記のスクリプトの応用のみ!
2.相関係数とは
2つのデータセットが与えられた時、散布図を書くとなんとなく右肩上がりや左肩上がりの分布が見える時がある。
たとえばいま使っているデータでは、CTDの塩分(3列目)とボトル塩分(4列目)を用いて散布図を書くと、
明らかに右肩上がりの分布図が見られる(図1)。
これは2つの変量の間に「正の相関」があることを示している。
※ただしこれだけではセンサーの精度がよいということにはならない。

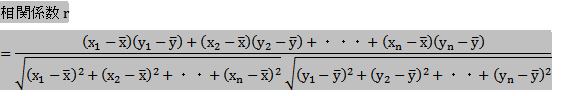
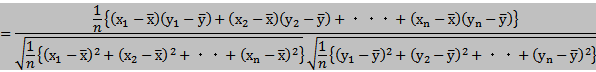
 ---- ①
---- ①
結局、2変数の共分散をそれぞれの変数の標準偏差で割ると、相関係数が得られるということである。
さてこの相関係数はいったい何者か?
根本原理はベクトルの内積にあります。思い出しましょう。
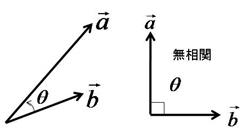
これを変形すると
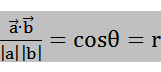 ---- ②
---- ②
この②式は実は①式と同じであります。
つまりaベクトルをCTD塩分の平均値からのズレ、bベクトルをボトル塩分の平均値からのからのズレと考えればよい。
n次元のベクトルを a=(a1,a2,a3,....), b=(b1,b2,b3,....)とおくと内積は以下のようになる
内積=a1b1+a2b2+a3b3+・・・・anbn
となる。これをnで割れば共分散になる。
次にn次元のベクトルの大きさは
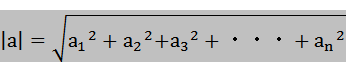
ベクトルbについても同じ。これらは①式の分母に相当する。
ここからは図1にある一次の回帰式を求める。
下図のように実測値と予測値の差が最小になるような傾き・切片を持つ回帰式を求める。
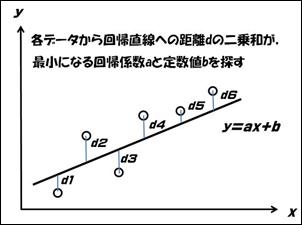
図3:回帰直線のイメージ
図2のd1(x1, y1)で考えてみる。d1の直上にある回帰直線のy座標は「ax1+b」になる。
従ってd1から回帰直線までの距離は
{y1 - (ax1+b)}
で表される。今回の場合も、距離の大きさを考えるのだから、二乗して総和を求める。
距離の二乗和をSとすると,
![]()
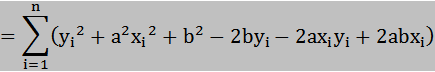
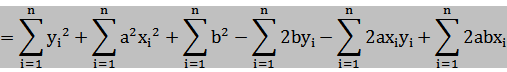
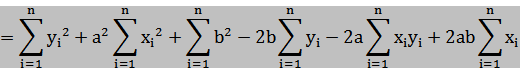
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ----④
----④
つまり距離の二乗和Sは「傾きa」と「切片b」の2次関数になる。
仮にaを固定するとbの二次関数である。
二次関数の最小値とは、傾きがゼロになる部分であるから、
上式④をa,bで偏微分したものがゼロになると置けばよい。
![]() ----⑤
----⑤
![]() ----⑥
----⑥
連立方程式から傾きaと切片bは以下のようになる。
![]() ----⑦
----⑦
![]() ----⑧
----⑧