
環境システム科学演習− MATLABを用いた海洋情報処理・作図演習
5) 最適内挿法を用いた海洋観測データの空間補間
5-1 最適内挿法-客観補間法
今、空間的にばらついた観測データd(xb)が存在している。これらのデータは複数の観測点xbで観測された。この観測値をその近傍である複数の点xaで推定することを考える。推定値Dと誤差n、元データdには以下の関係がある。

また、推定値DをDの平均と元データd、dの平均、重みwを用いて表す。即ち、ある推定地点における推定値は、全ての元データの情報に重みを付けて表すことが出来ると仮定する。
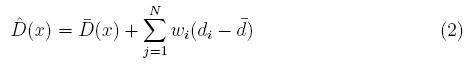
ここで重みの形は未だわかっていない。ただ、異なる重みが各推定地点毎に存在している。これを行列で書くと以下のようになる。
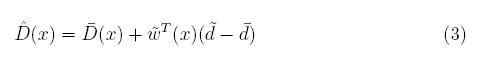
また、(3)式のDを一行の行列とした場合、以下も成り立つ。
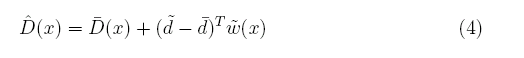
最小自乗と同様な考え方で、誤差をその自乗で見積もることを考える。即ち、

ここで、Dはある推定点1点における真の値、Dハットは、その推定点での推定値である。推定点は複数あるのでその平均で誤差の自乗とする。(4)式をある推定点一点について用いれば誤差の自乗は以下のように表せる。

推定を行う点1点におけるであるので、重みwとデータd-dバーの内積は順序を入れ替えられる。これを整理すると、
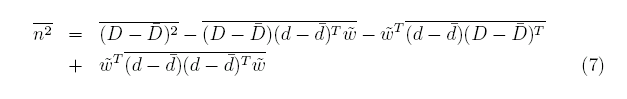
となる。また、Cが対称行列のときに成立する以下の法則を用いよう。

ここで、行列A、Bと対称行列Cを(5)式中の項から以下のように当てはめる。
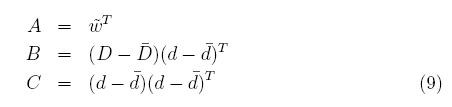
(7)式はさらに以下のように書くことが出来る。また、簡単の為BとCをCmd、Cddと定義する。これらのうちCmdはモデル点における真のデータ値と観測データとの共分散行列、Cddは観測データ自身の共分散行列である。

共分散行列とは即ち、

のように例えばAをモデル点毎の真の値(測定していないので知る由もないが)、Bを観測点毎の
観測値とするとき、AとBの共分散行列は、

のようにデータ数で正規化されないものをここでは指すこととする。
上記の行列の法則を当てはめて誤差の自乗を整理すると、

となる。この誤差の自乗を最小にするwを求めたい。ここで右辺第2項はモデル点におけるデータ真値とモデル値との差の自乗で常に正かつwには依存しない。第3項もwには依存しない。残された第2項は常に正であることが知られるため、これを0にするwを求めればよいことになる。或は第2項をwで微分することを考える。簡単のために、あるモデル点1点における誤差の自乗を考える。
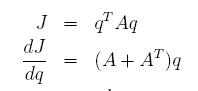
上記の微分法則において正方行列Aを正方行列Cddとしqを![]() としよう(地点が1点なのでqは列ベクトルとなる)。まずqで微分した後、qをwで微分すれば、誤差の自乗を最小にするwは、以下の関係を満たすことが判る。
としよう(地点が1点なのでqは列ベクトルとなる)。まずqで微分した後、qをwで微分すれば、誤差の自乗を最小にするwは、以下の関係を満たすことが判る。

したがって(3)式の未知数wを書き換えて以下のようになる。
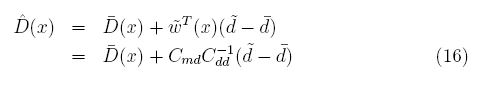
5-2 最適内挿法の利用
さて、(14)式が導けたので簡単にモデル点における推定値が求まるかのように見えるが実はまだ未知数が残っている。それはCmdでモデル地点における真の値と観測地点における観測値との共分散行列である。これはモデル地点における真の値は計っていないので知ることが出来ない為である。そこで、Cmdは通常Cddをある関数を用いて近似する方法がとられる。Cddについてもモデル値自身から導くこともあるし、観測地点の距離の関数として表すこともある。要は、共分散行列であるので距離的に近い観測点の共分散、即ち相関を大きくしておくということである。この演習では、Cdd、Cmdともに距離の関数として求めよう。例えば、以下のように共分散行列を距離0で共分散が1となり距離が離れれば正規分布のような分布で共分散が減衰していくような関数を当てはめてみることにする。

以下のx,y座標データのような場所に散らばる水温の観測値をこの共分散モデルにて最適内挿してみる。
xのデータ。
| 1 | 3 | 4 | 2 | 5 | 7 | 8 | 9 | 5 | 3 |
yのデータ。
| 5 | 5 | 1 | 4 | 8 | 2 | 6 | 7 | 1 | 9 |
水温のデータ。
| 8.0 | 11.0 | 11.5 | 9.0 | 7.0 | 11.0 | 8.5 | 7.5 | 12.0 | 5.0 |
距離はsqrt((x2-x1)2+(y2-y1)2)で算出することが出来るが、10点のデータの距離を基にした共分散の計算に用いる為10X10=100通りの距離の計算を行う必要がある。すなわちN点の座標から全ての組み合わせ(約半分は対称)でなす距離の行列を作らなければならない。
r=
| r11 | r12 | ... | r1N |
| r21 | r22 | ||
| ... | .. | ||
| rN1 | rNN |
このためまず座標を以下のようにN行N(M)列の行列にする。(ここでNは観測点数、Mは推定地点数)
xについて
X1=
| x1 | x2 | ... | xN |
| x1 | x2 | ... | xN |
| ... | ... | .. | ... |
| x1 | x2 | ... | xN |
X2=
| x1 | x1 | ... | x1 |
| x2 | x2 | ... | x2 |
| ... | ... | .. | ... |
| xN | xN | ... | xN |
yについて
Y1=
| y1 | y1 | ... | y1 |
| y2 | y2 | ... | y2 |
| ... | ... | .. | ... |
| yN | yN | ... | yN |
Y2=
| y1 | y2 | ... | yN |
| y1 | y2 | ... | yN |
| ... | ... | .. | ... |
| y1 | y2 | ... | yN |
したがって上記の様な行列rはX,Yをもちいてr=sqrt((X2-X1)2+(Y2-Y1)2)のように求めることが出来る。このrを用いれば共分散行列CddやCmdを(17)式を当てはめ求めることが容易である。CddとCmdが求まれば、Cmd Cdd-1を計算することで、誤差を最小にする重みが求まることになる。以下は上記データを(17)式を用いて最適内挿法によって補間する例である。

これを実行すると、以下の様な図が得られる。

丸でプロットされているのは、もとのデータである。
5-3 最適内挿法の演習課題
以下のリンクから、亜寒帯フロント域の水温の表層データをダウンロードし、相関距離50kmで最適内挿法を用いてデータを補間しよう。補間する格子や共分散モデルは各自自由にモデル化してください(上記例をそのまま用いても良い。あるいは、実際のデータの共分散を元にして共分散モデルを最小自乗法を用いて近似させるなどすると尚良い)。
格納変数:
tempd: 水温データ
xd: x座標データ
yd y座標データ
観測データは以下の様に分布している。
