
ここでfはコリオリパラメタ、vは南北方向の流れ、uは東西方向の流れ、pは水圧、ρは海水密度である。今、(1)と(2)をzで偏微分する。
環境システム科学演習− MATLABを用いた海洋情報処理・作図演習
4) MATLABを用いた海洋観測データ処理 地衡流計算と図示
地衡流計算は現場密度(比容)のデータから等圧面の傾斜を算出し、基準面から流速差を積分して観測面に直角な方向の地衡流をもとめる計算である。ここでは、その地衡流の概念について、またどのように地衡流計算を行うかについて学び、これまでに習得したプログラムも用いて地衡流計算法を習得する事を目標とする。
4-1 地衡流とは
流れが定常で、移流項と粘性項が無視できる時、また鉛直方向の平均流が小さいとき、水平的な運動を記述する運動方程式は以下のように書ける。

ここでfはコリオリパラメタ、vは南北方向の流れ、uは東西方向の流れ、pは水圧、ρは海水密度である。今、(1)と(2)をzで偏微分する。
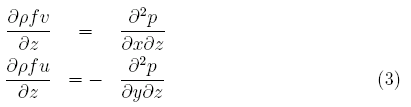
以下の静水圧の式を適用すると、

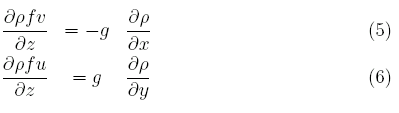
のようになる。これは温度風平衡の式と呼ばれ、水平方向の密度の勾配は、鉛直方向の流速の勾配と比例関係にあることを示している。海水の密度が大きい場合、単位質量当りの海水が占める体積は、密度が小さい場合よりも小さい。合計が同じ重さの水柱を考えたとき、密度の大きい海水の水柱の方が高さが低いことになる。密度の違いによらず海面での水圧は0であるので、密度が異なる二つの水柱の海面=等圧面は傾いている(差がある)といえる。判りやすいように密度一様の場合を考えよう。

図4−1
上図における点Aでの水圧は、-ρgη1で、Bでも同様に-ρgη2となる。これが南北方向の断面であるとし(2)式右辺の圧力勾配を2点間の距離Lを用いて近似すると、g(η2-η1)/Lと書ける。これが、fuとバランスしているので、u=g(η2-η1)/(Lf)として地衡流流速を求めることが出来る。したがって、海面(等圧面)の傾きを知ることが出来れば、海面の地衡流を知ることが出来る。しかしながら、大スケールの海面の傾きを船舶を用いた現場観測から明らかにすることはできない(最近では、絶対力学高度を人工衛星から測定することが可能となった)。そこで、古くから海洋学では海水の密度を異なる点で鉛直的に観測し、等圧面の水平的な傾きを密度の逆数を使って推定する手法が用いられた。上記の例では密度が一様なので単純であるが、実際の海洋は鉛直方向に密度が著しく変化するので、若干方法が複雑になる。
4-2 地衡流計算(力学計算)

成層している状態を想定し、地衡流計算について考えよう。今上図の観測点AとBにて水温、塩分、圧力の観測が行われたとする。地衡流計算では、この測点間をつなぐ線に直角な方向の流速勾配を知ることが可能である。そのためには、Φで示された水平面(ボールを置いても平らだから転がらない面)に対して等圧面がどれ位傾いているかを知らなければならないが、現場観測では直接知ることは出来ない。
図では、等圧面p1は、点A1、A2をとおり、p2はA2、B2を通って傾いている。そして海面はp0は大気圧となり、A,B点を通っていてこれも傾いている。今、p0、p1、p2面での地衡流速をV0、V1、V2としよう。すると、V1とV2について以下の式が書ける。

ここで、iは等圧面が水平面から傾いている角度である。この(7)から(8)を引くと、
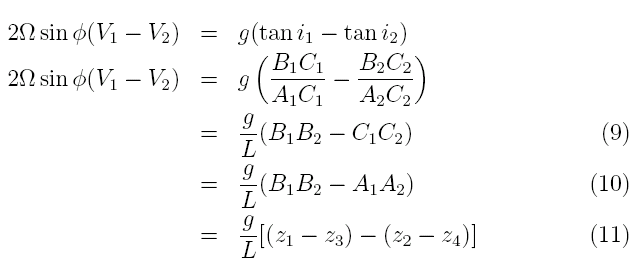
の関係が得られる。ここで、LはA1C1=A2C2=Lである。また、B1C1-B2C2=B1B2-C1C2を用いて(9)が導かれる。さらに、C1C2=A1A2であるので(10)が得られる。次に静水圧の式(4)から、以下のB点での重力加速度の鉛直軸に対する積分と比容の圧力に関する積分との関係が導かれる。

ここでαは密度の逆数、比容で単位質量あたりの海水が占める体積である。この比容の圧力に関する積分は、上式のようにα(35,0,p):塩分35、水温0℃、圧力pの比容成分とそれ以外を示すδに分ける。つまり、

(13)の右辺第2項以降を全てδとして表す。このδは、どれ位海水の比容が塩分35、水温0℃、圧力pの比容からずれているかを表すので、比容のアノマリーと呼ばれる。一方α(35,0,p)は圧力のみの関数で、圧力さえ与えられれば経験式から即座に求めることが出来る。(12)と同様に点Aについての式を求めると以下のようになる。
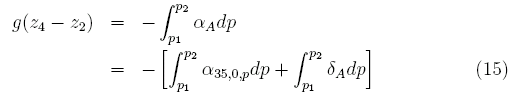
そして(15)を(12)から引くと、
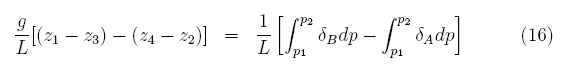
となり(11)式を比容のアノマリーで示すことが出来た。したがって上層と下層の流速差は以下のように定式化できる。
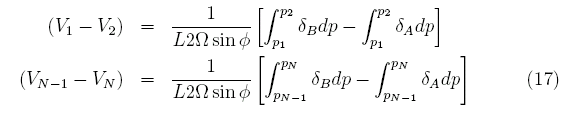
即ち、比容のアノマリーを圧力に関して積分し隣の点と比べることで、その下の層との流速差を求めることが出来る。2層だけでなく多層で、深層で流れを0とおくと(無流面の仮定)1層ずつ(17)のように流速として求めることが出来る。
一般的に用いられる実際の計算方法は、
1 各層の比容のアノマリを計算し、その層で圧力について積分。

2 その各層の積分値を最下層から積分する。
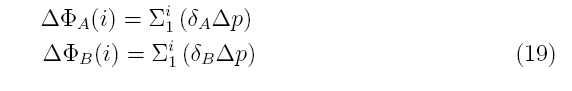
3 積分値を測点間で引き算し、各層の値をLとfで割ったものが地衡流流速となる。

ここでfは2ΩsinΦで求められるコリオリパラメータである。
4-3 2測点間の地衡流の計算例
| P | T | S | T | S | |
| 0 | 5.99 | 33.71 | 13.04 | 35.62 | |
| 25 | 6.00 | 33.78 | 13.09 | 35.63 | |
| 50 | 10.30 | 34.86 | 13.07 | 35.63 | |
| 75 | 10.30 | 34.88 | 13.05 | 35.64 | |
| 100 | 10.10 | 34.92 | 13.05 | 35.62 | |
| 150 | 10.25 | 35.17 | 13.00 | 35.61 | |
| 200 | 8.85 | 35.03 | 12.65 | 35.54 | |
| 300 | 6.85 | 34.93 | 11.30 | 35.36 | |
| 400 | 5.55 | 34.93 | 8.30 | 35.09 | |
| 600 | 4.55 | 34.95 | 5.20 | 34.93 | |
| 800 | 4.25 | 34.95 | 4.20 | 34.92 | |
| 1000 | 3.90 | 34.95 | 4.20 | 34.97 |
比容のアノマリを求めるには、前回用いたsigma_p.mを使おう。

ここでflipud(a)はa列ベクトルの上下を逆にします。
cumsum(a)はベクトルの累積和を求めます。
>> plot(V,-P)
で以下のような結果を図示できる。
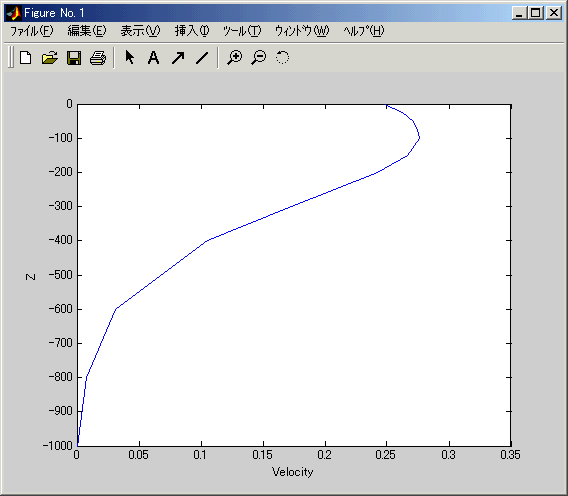
課題: 複数観測点間の地衡流計算
以下のリンクから水温、塩分の断面データファイルをダウンロードし、地衡流計算を行ってそれを図示しよう。図示にはcontourというMatlab functionを用いよう。
contourの使い方。
>>A=rand(5,5); %これで5行5列の乱数を生成、この等値線を引こう
>>[c,h]=contour(0:2:8,0:2:8,A,15,'k'); %黒い等値線15本をx,y座標「0-8(X) 0-8 (Y)」の範囲に書く
>>clabel(c,h) %等値線にラベルを自動挿入