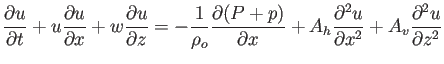 |
(1) | ||
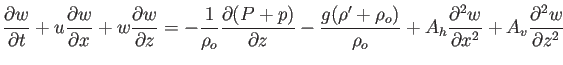 |
(2) | ||
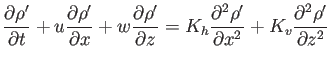 |
(3) |
�����ŁAu, w�́A���ꂼ��x, z�����̗����At�͎��ԁAP�͈�薧�x![]() �ƐÐ����̊W(
�ƐÐ����̊W(
![]() )�ɂ��鈳�́Ap�͈��͂�P����̕ϓ������A
)�ɂ��鈳�́Ap�͈��͂�P����̕ϓ������A![]() ,
, ![]() �́A���̊���x�Ƃ�������̕ϓ��AAh, �@Av�́A�����E�����̉Q�S���W���AKh, �@Kv�́A�����E�����̉Q�g�U�W���ł���Bx-z�ʂłQ�����̗�������肵�Ă���̂ŁA�k�̉���ɂ��Ƃ������x�ۑ���(�A���̎�)�́A
�́A���̊���x�Ƃ�������̕ϓ��AAh, �@Av�́A�����E�����̉Q�S���W���AKh, �@Kv�́A�����E�����̉Q�g�U�W���ł���Bx-z�ʂłQ�����̗�������肵�Ă���̂ŁA�k�̉���ɂ��Ƃ������x�ۑ���(�A���̎�)�́A
�ł���B�A���̎������藧���́A����𗬐����A![]() �A�̌��z�Ƃ��ĕ��鎖���Ӗ�����B�����A
�A�̌��z�Ƃ��ĕ��鎖���Ӗ�����B�����A
���A�Q�x![]() ��
��
�ƒ�`����A![]() ��
��![]() �́A�ȉ��̎������B
�́A�ȉ��̎������B
���̗������ƉQ�x��p���āA��(11)��(21)�́A(1)��z��(2)��x�ŕΔ������A���������Έ��͍��������ł��A��ɂ܂Ƃ߂邱�Ƃ��ł���B���̉ߒ��ŁA�Ð����̎���p����B�]���āA�V� �����[�V�����ɗp����������͈ȉ��̗l�ɂȂ�B
���E������x�ɂ��Ď����I���E����
���̗p����Bz�ɂ��ẮA�ǂ𗬂ꂪ����Ȃ������A�X�g���X���E�������̗p���������ŕǂ���̉^���ʁA���x�t���b�N�X���Ȃ������A