最大公約数GCM

最大公約数とは、二つの自然数を割って割り切れる最大の自然数である。下の例では、aをbで割って商がc、余りがrになる例である。 次に、自然数a=68, b=24の場合を考える。 まず大きな数字68を小さな数字24で割る。商は、2、余りは20である。

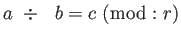$$a \div  b= c  (\bmod : r )$$ (2)

$$68 \div 24 = 2 (\bmod : 20)$$

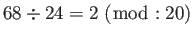もし、68が24で割り切れたら24は24でも割り切れるので、24が最大公約数であるが、実際は上の様に割り切れない。 ここで、

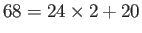$$68 = 24 \times 2 + 20$$ (3)

と書き直せる。

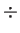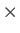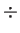仮に最大公約数をXとすれば、68$\div$Xの余りは0、24$\times$2$\div$Xの余りも0、20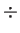$\div$Xの余りも0でなければならない。

即ち、68と24の最大公約数は、24ではないが、24と20の最大公約数とも言える。

したがって、同様に24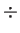$\div$20を行い、もし割り切れれば20が最大公約数Xとなる。しかしこれも割り切れない。

これは商が1余りが4である。そこで、今度は20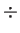$\div$4を行い、これは割り切れるので最大公約数Xは4となる。 これは68と24の最大公約数に等しい。

以上のことから最大公約数を求めるには、

• aとbの入力
• aをbで割り、余りが0なら最大公約数をbとする。(4)に飛ぶ。
• 余りが0で無いなら、aをbで置き換え、余りbをaとする。(2)へ戻る。
• 最大公約数を表示させる。