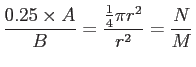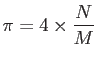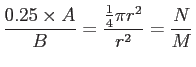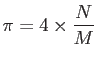Next: グラフィック
Up: GOSUB 関数副プログラムを用いる
Previous: Sample Program 10
Contents
円の面積Sは を半径として
を半径として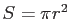 で表される。
で表される。 と
と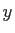 をそれぞれ横軸、縦軸として、第一象限(
をそれぞれ横軸、縦軸として、第一象限(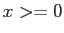 ,
, 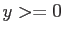 )に現れる円の面積は、当然この4分の1、
)に現れる円の面積は、当然この4分の1、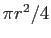 である。今
である。今 と
と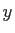 という[0 1]までの乱数を無数に発生させると、半径
という[0 1]までの乱数を無数に発生させると、半径 の円の内側にこの(
の円の内側にこの(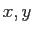 )座標が入る確率は、原点が一つの角と接する一辺の長さ1の正方形の面積で4分の1円で割ったものに等しい。従って、円の内側に入った乱数座標の個数/全ての乱数の個数=0.25S/正方形の面積。即ち、
)座標が入る確率は、原点が一つの角と接する一辺の長さ1の正方形の面積で4分の1円で割ったものに等しい。従って、円の内側に入った乱数座標の個数/全ての乱数の個数=0.25S/正方形の面積。即ち、
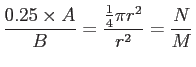 |
|
|
(1) |
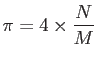 |
|
|
|
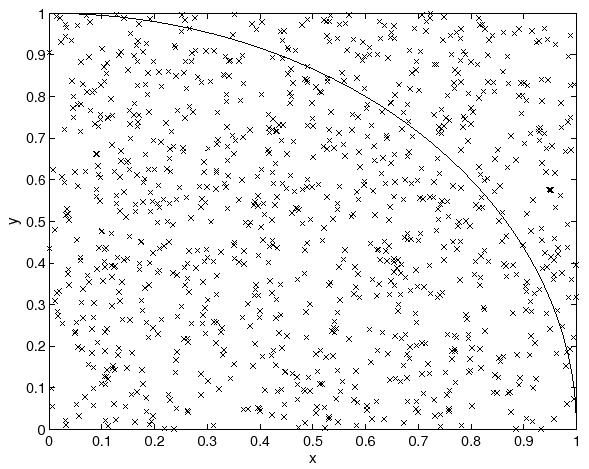
である。ここで、Aは円の面積、Bは正方形の面積です。Nは4分の1円に入った乱数の数、Mは全乱数の数です。この関係を模式図で表すと以下の通りである(図の参照 10.2)。この関係と、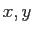 座標を表す乱数を1000個程度用いて、piを求めるプログラムを作成せよ。算出されたpiを乱数の個数を幾つか変えてその変化について述べよ。ただし、円周上の座標は
座標を表す乱数を1000個程度用いて、piを求めるプログラムを作成せよ。算出されたpiを乱数の個数を幾つか変えてその変化について述べよ。ただし、円周上の座標は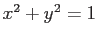 であり、ここで、
であり、ここで、 と
と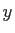 は乱数で表そうとする座標である。作成するプログラムでは、必ず
は乱数で表そうとする座標である。作成するプログラムでは、必ず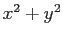 を算出する副プログラムとgosubを用いること。たとえば、
を算出する副プログラムとgosubを用いること。たとえば、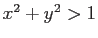 なら、この乱数で示される点は、円の外にあることになる。
提出はここからログインして行って下さい。
なら、この乱数で示される点は、円の外にあることになる。
提出はここからログインして行って下さい。
Figure 3:
乱数の示す座標と円、正方形の関係の模式図。
 |
Takeyoshi Nagai
2017-01-23