



Next: 演習例題
Up: 環境システム科学演習ーEOF解析
Previous: Contents
Contents
今、海面水温偏差の時系列データ(1-N個)が、1-M個の観測点で得られる場合を考える。この観測データが示す
変動を互いに直交し相関を持たないM個の関数(モード)の線形結合として聞ことを考える。(これは、
時系列データを無数のフーリエ直交関数で聞のと類似しているが、この場合、とられる関数
の形は三角関数に限定されず、関数の形自体もデータから求めることになる。)即ち、
![$\displaystyle \psi_m(t) = \sum_{i=1}^M [a_i(t)\phi_m^i].$](img1.png) |
(1) |
ここで、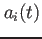 は、時刻tにおけるi番目のモードの振幅を雰、
は、時刻tにおけるi番目のモードの振幅を雰、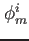 、は観測点
mにおけるi番目のモードの関数値を与える。全変動は、これらモードの総和として併るとする。
総和として併るということは、各モード間での掛け算が、それ自身との掛け算以外0になる
ことを意味する。即ち、モード間での相関はなく、それ故
、は観測点
mにおけるi番目のモードの関数値を与える。全変動は、これらモードの総和として併るとする。
総和として併るということは、各モード間での掛け算が、それ自身との掛け算以外0になる
ことを意味する。即ち、モード間での相関はなく、それ故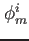 は、直交関数と呼ばれる。即ち、
は、直交関数と呼ばれる。即ち、
![$\displaystyle \sum_{m=1}^M [\phi_{im}\phi_{jm}]=\delta_{ij},$](img4.png) |
(2) |
を意味する。ここで
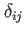 は、クロネッカーデルタとよばれ、
は、クロネッカーデルタとよばれ、
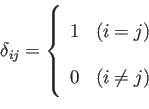 |
|
|
(3) |
を満たし、あるモード自身との掛け算は、それ以外は0である。各モードの振幅、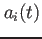 もモード間で相関が無いとしなければモードの変動の総和でデータを聞ことができなくなってしまう。
即ち、
もモード間で相関が無いとしなければモードの変動の総和でデータを聞ことができなくなってしまう。
即ち、
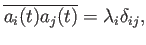 |
(4) |
ここで
 は、時間平均を示す。また
は、時間平均を示す。また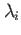 は、
は、
![$\displaystyle \lambda_i=\overline{a_i(t)^2}=\frac{1}{N}\sum_{k=1}^N [a_i(t_k)^2],$](img10.png) |
(5) |
であり、時系列データ、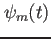 から平均値を差し引いたものを取り扱っている場合、
から平均値を差し引いたものを取り扱っている場合、
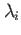 は、偏差データの各モードにおける振幅の分散に等しい。
は、偏差データの各モードにおける振幅の分散に等しい。
さて、(1)を行列を用いて聞と、以下の様に併る。
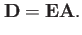 |
(6) |
即ち、
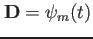 とおき、
とおき、
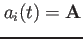 、
、
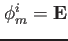 とした。
行列の式のかたちは以下の様に聞ことができる。
とした。
行列の式のかたちは以下の様に聞ことができる。
![$\displaystyle \left[ \begin{array}{ccccc} \psi_{11} & \psi_{12} & \psi_{13} & ....
...& :& : & ... & : a_{M1} & a_{M2} & a_{M3} & ... & a_{MN} \end{array} \right]$](img16.png) |
(7) |
右辺の行列のかけ算によって、
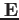 のi行目と、
のi行目と、
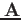 のj列目が要素それぞれの積の総和として求まる。このとき、
行列の次元を確認すると、
のj列目が要素それぞれの積の総和として求まる。このとき、
行列の次元を確認すると、
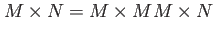 であるので、2つの行列のかけ算
によって両者の内側の次元が消える事がわかる。また内側の次元は等しくなければならない。
であるので、2つの行列のかけ算
によって両者の内側の次元が消える事がわかる。また内側の次元は等しくなければならない。
今、式(6![[*]](file:/usr/share/latex2html/icons/crossref.png) )の両辺に
)の両辺に
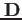 の転置行列、
の転置行列、
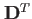 を右から掛ける。即ち、
を右から掛ける。即ち、
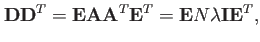 |
(8) |
ここで、
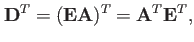 |
(9) |
および、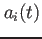 が線形独立(それ自身以外とのかけ算が0、
が線形独立(それ自身以外とのかけ算が0、
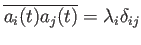 の関係を用いた。
の関係を用いた。
また、ここで、
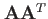 が、式(4
が、式(4![[*]](file:/usr/share/latex2html/icons/crossref.png) )の
)の
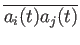 にデータ数、
にデータ数、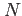 をかけたものに等しいため、
をかけたものに等しいため、
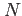 を付与しなければならない。今、以下の形をとる式(8
を付与しなければならない。今、以下の形をとる式(8![[*]](file:/usr/share/latex2html/icons/crossref.png) )の右辺
)の右辺
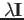 を、
を、
![$\displaystyle N\lambda \mathbf{I}= N\left[ \begin{array}{ccccc} \lambda_{11} & ...
...a_{M-1 M-1} & 0 0 & 0 & 0 & ... & \lambda_{MM} \end{array} \right]=\mathbf{L}$](img29.png) |
(10) |
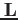 と定義する。Lは対角行列であるので、
と定義する。Lは対角行列であるので、
 が成立する。このため、
が成立する。このため、
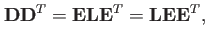 |
(11) |
がなりたつ。今、式(11![[*]](file:/usr/share/latex2html/icons/crossref.png) )の右からEをかけると、
)の右からEをかけると、
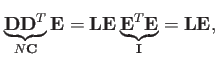 |
(12) |
となる。(
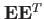 は
は
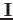 にはならないことに注意。)ここで、
にはならないことに注意。)ここで、
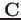 は、
データの共分散行列である。式(
は、
データの共分散行列である。式(![[*]](file:/usr/share/latex2html/icons/crossref.png) 12)を行列成分まで書くと以下の様な形になる。
12)を行列成分まで書くと以下の様な形になる。
![$\displaystyle N\left[ \begin{array}{ccc} C_{11} & ... & C_{1M} : & ... & : \...
.... & \phi_{1M} : & ... & : \phi_{M1} & ... & \phi_{MM} \end{array} \right]$](img37.png) |
(13) |
これを各観測点 について、式を書くと、
について、式を書くと、
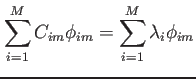 |
(14) |
となりこれは、固有値: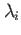 、固有ベクトル:
、固有ベクトル: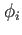 の固有値問題である。
の固有値問題である。
ところで、最初の定義で、
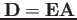 でデータを線形モードの総和で
塀うとした。この式の両辺の左から
でデータを線形モードの総和で
塀うとした。この式の両辺の左から
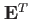 をかけると、
をかけると、
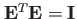 であるので、整理すると
であるので、整理すると
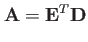 |
(15) |
となり、任意の時間、観測点における各モードの振幅は、
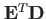 として
得られることが分かる。即ち、データの共分散を求めた後、式(12
として
得られることが分かる。即ち、データの共分散を求めた後、式(12![[*]](file:/usr/share/latex2html/icons/crossref.png) )の固有値問題を解いて
)の固有値問題を解いて
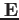 (固有ベクトル)と
(固有ベクトル)と
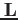 (固有値)を求められるが、さらに求めた
(固有値)を求められるが、さらに求めた
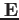 から振幅
から振幅
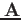 を求められる。したがって、最初の式:
を求められる。したがって、最初の式:
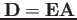 を用いて
任意の時間、観測点における各モードの振る舞いを抽出することができる。
を用いて
任意の時間、観測点における各モードの振る舞いを抽出することができる。




Next: 演習例題
Up: 環境システム科学演習ーEOF解析
Previous: Contents
Contents
Takeyoshi Nagai
2011-11-29
![$\displaystyle \psi_m(t) = \sum_{i=1}^M [a_i(t)\phi_m^i].$](img1.png)
![]() は、時刻tにおけるi番目のモードの振幅を雰、
は、時刻tにおけるi番目のモードの振幅を雰、![]() 、は観測点
mにおけるi番目のモードの関数値を与える。全変動は、これらモードの総和として併るとする。
総和として併るということは、各モード間での掛け算が、それ自身との掛け算以外0になる
ことを意味する。即ち、モード間での相関はなく、それ故
、は観測点
mにおけるi番目のモードの関数値を与える。全変動は、これらモードの総和として併るとする。
総和として併るということは、各モード間での掛け算が、それ自身との掛け算以外0になる
ことを意味する。即ち、モード間での相関はなく、それ故![]() は、直交関数と呼ばれる。即ち、
は、直交関数と呼ばれる。即ち、
![]() は、クロネッカーデルタとよばれ、
は、クロネッカーデルタとよばれ、
![]() もモード間で相関が無いとしなければモードの変動の総和でデータを聞ことができなくなってしまう。
即ち、
もモード間で相関が無いとしなければモードの変動の総和でデータを聞ことができなくなってしまう。
即ち、
![]() とおき、
とおき、
![]() 、
、
![]() とした。
行列の式のかたちは以下の様に聞ことができる。
とした。
行列の式のかたちは以下の様に聞ことができる。
![]() が、式(4
が、式(4![]() )の
)の
![]() にデータ数、
にデータ数、![]() をかけたものに等しいため、
をかけたものに等しいため、
![]() を付与しなければならない。今、以下の形をとる式(8
を付与しなければならない。今、以下の形をとる式(8![]() )の右辺
)の右辺
![]() を、
を、
![]() について、式を書くと、
について、式を書くと、
![]() でデータを線形モードの総和で
塀うとした。この式の両辺の左から
でデータを線形モードの総和で
塀うとした。この式の両辺の左から
![]() をかけると、
をかけると、
![]() であるので、整理すると
であるので、整理すると